Abstract

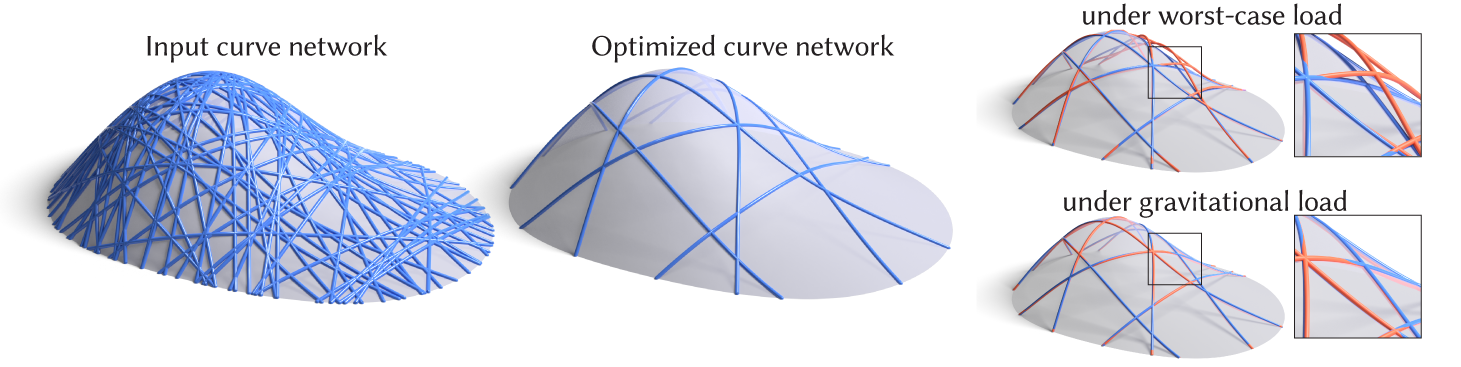
Designing curve networks for fabrication requires simultaneous consideration of structural stability, cost effectiveness, and visual appeal—complex, interrelated objectives that make manual design a difficult and tedious task.
We present a novel method for fabrication-aware simplification of curve networks, algorithmically selecting a stable subset of given 3D curves. While traditionally stability is measured as magnitude of deformation induced by a set of pre-defined loads, predicting applied forces for common day objects can be challenging. Instead, we directly optimize for minimal deformation under the worst-case load.

Our technical contribution is a novel formulation of 3D curve network simplification for worst-case stability, leading to a mixed-integer semi-definite programming problem (MI-SDP). We show that while solving MI-SDP directly is infeasible, a physical insight suggests an efficient greedy approximation algorithm. We demonstrate the potential of our approach on a variety of curve network designs and validate its effectiveness compared to simpler alternatives using numerical experiments.

@article{Neveu:2022:curvenetworks,
author = {William Neveu and Ivan Puhachov and Bernhard Thomaszewski and Mikhail Bessmeltsev},
title = {Stability-Aware Simplification of Curve Networks},
journal = {ACM Transactions on Graphics},
year = {2022},
doi = {10.1145/3528233.3530711}
}